Multiscale interaction in geofluid flows
Let T (such as density or velocity components) be a scalar field in an incompressible fluid flow V. If both T and V vary in time, it is possible that energy be transferred from one scale window to another window, leading to the generation of coherent structures (such as eddies). In the framework of MWT, this transfer, written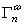 
, can be rigorously obtained （Liang & Robinson, 2005; 2007）：
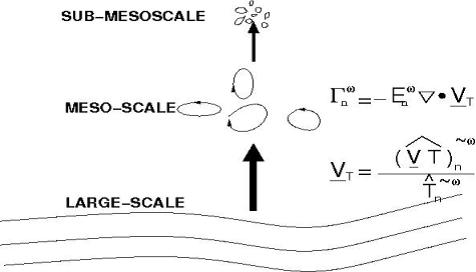
where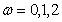 
signify, respectively, large-sclae, meso-scale, sub-mesoscale windows, n is time step, 
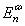is the energy of window , and 
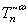(with a hat) is the MWT of T on scale window and time step n. The quantity 
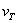, called T-coupled velocity, has the dimension of velocity. 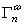has the following nice property:
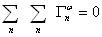
which means that this kind of transfer is just a redistribution of energy among scale windows; it does not generate nor destroy energy. This is quite different from the empirical/half-empirical formulas available so far. In distinction we call it canonical transfer.
In the above formulas, one can obtain the canonical transfers of kinetic energy and available potential energy if T is replaced by, respectively, velocity components and perturbation density. These two prove to precisely correspond to the classical barotropic instability and baroclinic instability in geophysical fluid dynamics, while no spatial averaging nor temporal averaging are taken, and hence can faithfully represent the real hydrodynamic instability processes which may be localized or intermittent in space and time.
Consider a barotropic zonal jet confined within two latitudes (-1<y/L<+1). For it to be unstable, two necessary conditions are required, i.e., the Rayleigh condition and the Kuo condition. Now consider a very special basic velocity profile (Fig. a), which as a whole meets these requirements, but the Kuo condition does not hold locally at the two inflection points in Fig. b (Fig. c). So by the theorems of Rayleigh and Kuo, the flow must be stable at least in the vicinity of these points.
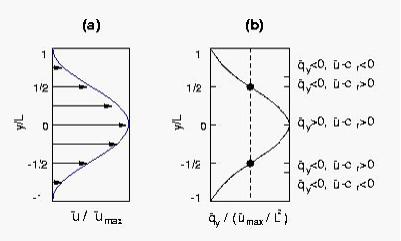
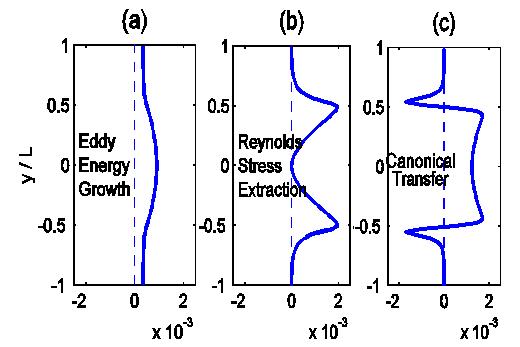
However, the calculated growth of perturbation energy (Fig. a, below) is positive at all latitudes; clearly, one cannot infer through observing the perturbation growth the underlying instability, at least the instability around the two inflection points. Alternatively it has been a common practice to make the inference by computing the energy extracted via Reynold stress against the basic profile, which we call Reynolds stress extraction henceforth. The computed extraction is plotted in Fig. b. To one’s surprise, it shows that the flow is most unstable around the two inflection points. This is at odds with the classical analytical results, and is obviously wrong. In contrast, the computed canonical transfer (Fig. c) accurately reproduces the structure of instability: Though the jet is unstable as a whole, it is stable in the neighborhood of the two inflection points, where energy is transferred inversely from the perturbation to the mean state.
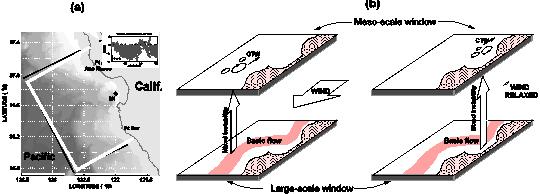
The above theory and methodology have been applied to several real ocean studies. Interestingly, many ocean problems, albeit seemingly complicated, may have simple dynamical processes lying beneath. An example is seen in the dynamical study of the Monterey Bay circulation (Liang & Robinson, 2009). Monterey Bay (Fig. a below) is a crescent-shaped embayment indented on the central California famous for its high productivity and marine life diversity. Oceanographers have invested enormous effort in understanding the dynamics of its complex circulation ever since 70 years ago, but the major processes are still not clear. Recently a breakthrough was made using the above theory and methodology. The complicated dynamical flow pattern is found to be governed by two instabilities, one within the Bay and another south of it. As shown in Fig. b below, when upwelling-favorable winds (northwesterly) blow, an instability, which is mixed in nature (i.e., both barotropic and baroclinic), occurs south of the Bay, and the resulting mesoscale eddies propogate northward in the form of coastal trapped waves; when the northwesterly is relaxed, the instability process ceases, but the flow within the Bay loses its stability (still mixed in nature), and the generated eddies also propagate northward, with oscillations mainly trapped around the thermocline. Besides, we have observed that the upwelling formation within the Bay does not follow the classical paradigm; it actually originates from nonlinear mixed instabilities. The role that the wind plays in driving the ocean is also different from the traditional scenario; it first stores energy in the large-scale window and then makes a transfer to the mesoscale window via hydrodynamic instabilities. This work, which has been touted by a referee as a "major advance" in dynamical diagnosis of the California Current System, is just the result of a straightforward application of our theory and methodology.
Click to download related articles：