Predictability theory
Theorem 1 (Liang & Kleeman, 2005; 2014): For a dynamical system du/dt = F(u,t), where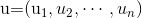 
, the time rate of change of its joint entropy H is the divergence of its vector field F followed by a mathematical expectation, i.e.,
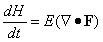
Remark: If u is the position vector, F is velocity; if u is a vector of the discretized state variables in a numerical atmosphere/ocean model, then F is the vector field formed by the model.
Theorem 2 (Liang, 2011): For the above system, let the marginal entropy of its kth component be Hk, the time rate of its static change (or local change), i.e., the change without taking into account the effect from other components due to event synchronization, is
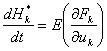
Remark: This quantity tells the growth of uncertainties intrinsic to the system, and is hence the appropriate measure of uncertainty generation. We call it Local Entropy Generation, or LEG for short.
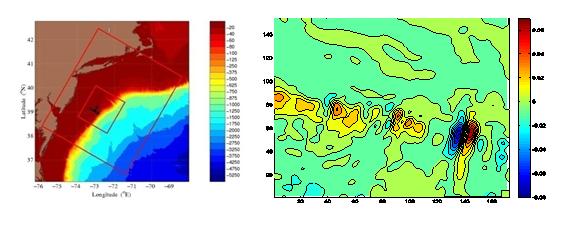
The above theorems can be easily employed to study the intrinsic sources in the atmosphere and/or oceans. In the following figures we show an example with the Mid-Atlantic Bight circulation in 2006 (Liang et al., 2011). The left figure marks the domain (the small one); the right (rotated clockwise by 60°for clarity) shows the LEG, with positive values indicating the uncertainty generation sources.
Click to download related articles：
X. San Liang, 2014: Entropy evolution and uncertainty estimation with dynamical systems. Entropy, 16, 3605-3634.